Understanding Bresenham’s Circle Drawing Algorithm in Computer Graphics

Summary

Sources

medium.com

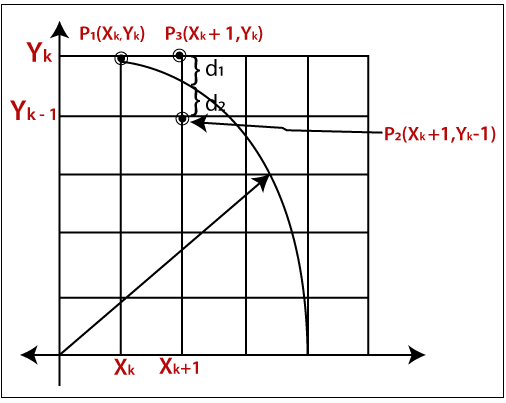
In the realm of computer graphics, efficient and accurate algorithms are essential for rendering geometric shapes. One of the fundamental tasks is drawing a circle, which appears in various applications, from simple graphical user interfaces to complex simulations. Bresenham’s Circle Drawing Algorithm is a well-known method for this purpose, celebrated for its efficiency and precision. Bresenham’s Circle Drawing Algorithm is an incremental scan conversion algorithm. It is an extension of Bresenham’s Line Drawing Algorithm, which was introduced by Jack E. Bresenham in nineteen sixty-two. The circle drawing algorithm, like its predecessor, is designed to use only integer arithmetic, making it particularly efficient for computer graphics, where floating-point operations can be costly. The core idea of Bresenham’s Circle Drawing Algorithm is to exploit the symmetry of the circle. A circle is symmetrical about its center, and any point on the circle satisfies the equation: x squared plus y squared equals r squared, where r is the radius of the circle. By plotting one-eighth of the circle and reflecting these points in the other octants, the algorithm can efficiently draw the entire circle. The algorithm uses decision parameters to determine the closest pixel to the theoretical circle circumference at each step, thus minimizing the error. It starts at the top of the circle and works its way down to the x-axis, plotting points in each octant simultaneously. The step-by-step process begins with initialization. Start with the circle’s center at the origin for simplicity. For a circle centered at a different point, adjust the coordinates accordingly. Define the radius and set the initial point at coordinates zero and the radius. Initialize the decision parameter to one minus the radius. Next, comes plotting points. For each point starting from coordinates zero and the radius, plot the point in all eight octants. Update the coordinates based on the decision parameter. If the decision parameter is less than zero, the next point is incremented in the x direction, and the decision parameter is updated by adding two times x plus one. If the decision parameter is greater than or equal to zero, the next point is incremented in the x direction and decremented in the y direction, and the decision parameter is updated by adding two times x minus two times y plus one. Utilizing symmetry, reflect the points plotted in the first octant to the other seven octants. Here is a simple implementation of Bresenham’s Circle Drawing Algorithm in C++: Include the graphics library appropriate for your environment. Define a function to plot the circle points. In the main function, initialize the graphics mode, call the Bresenham circle function with the center coordinates and radius, and then close the graphics mode. The advantages of Bresenham’s Circle Drawing Algorithm are notable. It is efficient, using only integer arithmetic, thereby avoiding computationally expensive floating-point calculations. The algorithm is accurate, determining the nearest pixel to the theoretical circle path. It is also simple to implement and understand. Bresenham’s Circle Drawing Algorithm is a powerful tool in computer graphics, providing an efficient and accurate method for drawing circles. By leveraging symmetry and utilizing integer arithmetic, it stands as a testament to effective algorithm design, ensuring high performance even on systems with limited computational resources. Understanding and implementing this algorithm is a valuable skill for anyone interested in computer graphics.